Count Inversion in An Array

Explaination

A pair (arr[i], arr[j]) form an inversion when:

• i < j and
• arr[i] > arr[j]

Examples

Input: [12, 14, 11, 13, 15]
Output: 3
Explaination: (14, 11), (14, 13), (12, 11)

Input: [11, 22, 44, 55]
Output: 0
Explaination: Array elements are sorted in increasing order then output will be zero

Input: [44, 33, 22, 11]
Output: 6
Explaination: Array elements are sorted in decreasing order then output will be maximum possible
(44, 33), (44, 22), (44, 11), (33, 22), (33, 11), (22, 11)

Naive Solution

package main

import (
    "fmt"
)

func main() {
    arr := []int{12, 14, 11, 13, 15} // output = 3
    // arr := []int{11, 22, 44, 55} // output = 0
    // arr := []int{44, 33, 22, 11} // output = 6
    res := inversionCount(arr)
    fmt.Println(res)
}

func inversionCount(arr []int) int {
    res := 0
    for i := 0; i < len(arr); i++ {
        for j := i + 1; j < len(arr); j++ {
            if arr[i] > arr[j] {
                res++
            }
        }
    }
    return res
}

Time Complexity: O(n * n)

Efficient Solution

Implementation

• The idea is based on merge sort
• We divide the array into two halves and we sort these two halves recursively then we merge these two halves. We count inversion while sorting the array
  • We count inversion in left half
  • We count inversion in right half
  • While merging, we count inversion where one element is from left half and one element from right half

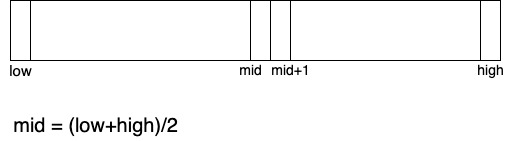
Every inversion (x,y) where x>y has three possibity
1. Both x & y are in left half
2. Both x & y are in right half
3. x is in left half and y is in right half

package main

import (
    "fmt"
)

func main() {
    arr := []int{12, 14, 11, 13, 15} // output = 3
    // arr := []int{11, 22, 44, 55} // output = 0
    // arr := []int{44, 33, 22, 11} // output = 6
    res := inversionCount(arr, 0, len(arr)-1)
    fmt.Println(res)
}

func inversionCount(arr []int, l, r int) int {
    res := 0
    if r > l {
        m := (l + r) / 2
        res += inversionCount(arr, l, m)
        res += inversionCount(arr, m+1, r)
        res += countAndMerge(arr, l, m, r)
    }
    return res
}

func countAndMerge(arr []int, low, mid, high int) int {
    n1 := mid - low + 1
    n2 := high - mid
    left := make([]int, n1)
    right := make([]int, n2)

    for i := 0; i < n1; i++ {
        left[i] = arr[low+i]
    }

    for i := 0; i < n2; i++ {
        right[i] = arr[mid+i+1]
    }

    res := 0
    i := 0
    j := 0
    k := low
    for i < n1 && j < n2 {
        if left[i] < right[j] {
            arr[k] = left[i]
            i++
        } else {
            arr[k] = right[j]
            j++
            // when an element found smaller in right array,
            // it means all element from ith in element of left array are also greater than that element.
            // so number inversion will also be number of element in left array from ith index
            res = res + n1 - i
        }
        k++
    }
    for i < n1 {
        arr[k] = left[i]
        i++
        k++
    }

    for j < n2 {
        arr[k] = right[j]
        j++
        k++
    }

    return res
}

Time Complexity: O(n * log n)
Aux Space Complexity: O(n)

Dry Run: -- TO BE DONE