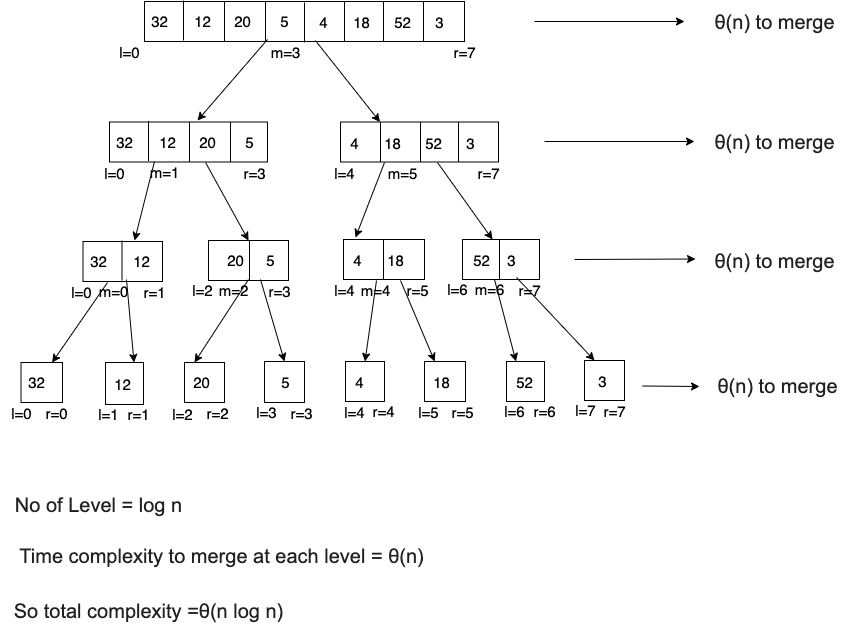
Merge Sort
Introduction
- Divide and Conquer Algorithm
- Divide
- Conquer
- Merge
- Stable Algorithm
- θ(n log n) time and O(n) aux space
- Well suited for linked list. Works in O(1) aux space
- Used in external sorting
- In generate for array. Quick sort outperforms it.
Merge Two Sorted Array
Input: a[] = {12, 17, 22} b[] = {7, 8, 8, 17} Ouput: c[] = {7, 8, 8, 12, 17, 22}
Input: a[] = {11, 11, 22} b[] = {33} Ouput: c[] = {11, 11, 22, 33}
Naive Solution
package main
import (
"fmt"
"sort"
)
type Person struct {
id int
name string
}
func main() {
a := []int{10, 15, 20, 20}
b := []int{1, 2, 13}
c := merge(a, b)
fmt.Println(c)
}
func merge(a []int, b []int) []int {
c := make([]int, len(a)+len(b))
for i, ele := range a {
c[i] = ele
}
for i, ele := range b {
c[len(a)+i] = ele
}
sort.Ints(c)
return c
}
Time Complexity: O((m+n) log(m+n)) Space Complexity: θ(m+n)
Dry Run: a[] = {10, 15, 20, 20} b[] = {1, 2, 13}
After 1st Loop: c[] = {10, 15, 20, 20, , , _} After 2st Loop: c[] = {10, 15, 20, 20, 1, 2, 13} After Sorting: c[] = {1, 2, 10, 13, 15, 20, 20}
Efficient Solution
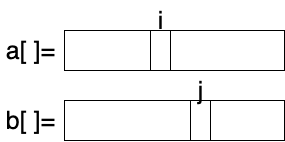
Initially i=0, j =0
if a[i] <= b[j] { append a[i]; i++} else append b[j]; j++
package main
import "fmt"
func main() {
a := []int{5, 10, 15, 20}
b := []int{10, 20, 30}
res := merge(a, b)
fmt.Println(res)
}
func merge(a []int, b []int) (result []int) {
i := 0
j := 0
for i < len(a) && j < len(b) {
if a[i] <= b[j] {
result = append(result, a[i])
i++
} else {
result = append(result, b[j])
j++
}
}
for i < len(a) {
result = append(result, a[i])
i++
}
for j < len(b) {
result = append(result, b[j])
j++
}
return
}
Time Complexity: θ(m+n)
Dry Run: a := {5, 10, 15, 20} b := {10, 20, 30}
First Loop i=0, j=0 c[]={5} i=1 c[]={5, 10} i=2 c[]={5, 10, 10} j=1 c[]={5, 10, 10, 15} i=3 c[]={5, 10, 10, 15, 20} i=4
Second Loop Nothing
Third Loop c[]={5, 10, 10, 15, 20, 20} j=2 c[]={5, 10, 10, 15, 20, 20, 30} j=3
Merge Function of Merge Sort
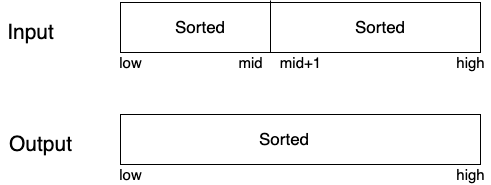
Input: a[] = {12, 15, 22, 13, 32} |---------| |-----| low = 0 mid = 2 high = 4
Output: a[] = {12, 13, 17 , 22, 32}
Input: a[] = {7, 10, 12, 14, 9}
|-------------| |--|
low = 0
mid = 3
high = 4
Output: a[] = {7, 10, 12, 14, 9}
Implementation Idea
a[] = {13, 18, 21, 45, 10, 15, 80} low = 0 mid = 3 high = 6 left[] = {13, 18, 21, 45} right[] = { 10, 15, 80}
merge left and right array
a[] = {10, 13, 15, 18, 21, 45, 80}
Implementation
func merge(a []int, low int, mid int, high int) {
// Setting up auxilary array
n1 := mid - low + 1
n2 := high - mid
left := make([]int, n1)
right := make([]int, n2)
for i := 0; i < n1; i++ {
left[i] = a[low+i]
}
for i := 0; i < n2; i++ {
right[i] = a[mid+i+1]
}
// standard merge logic
i := 0
j := 0
k := low
for i < n1 && j < n2 {
if left[i] < right[j] {
a[k] = left[i]
i++
k++
} else {
a[k] = right[j]
k++
j++
}
}
for i < n1 {
a[k] = left[i]
k++
i++
}
for j < n2 {
a[k] = right[j]
k++
j++
}
}
Time complexity: θ(n) Aux Space: θ(n)
Merge Sort Algorithm
func mergeSort(arr []int, l, r int) {
if r > l { // atleast 2 elements
m := (l + r) / 2
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)
}
}
Explaination
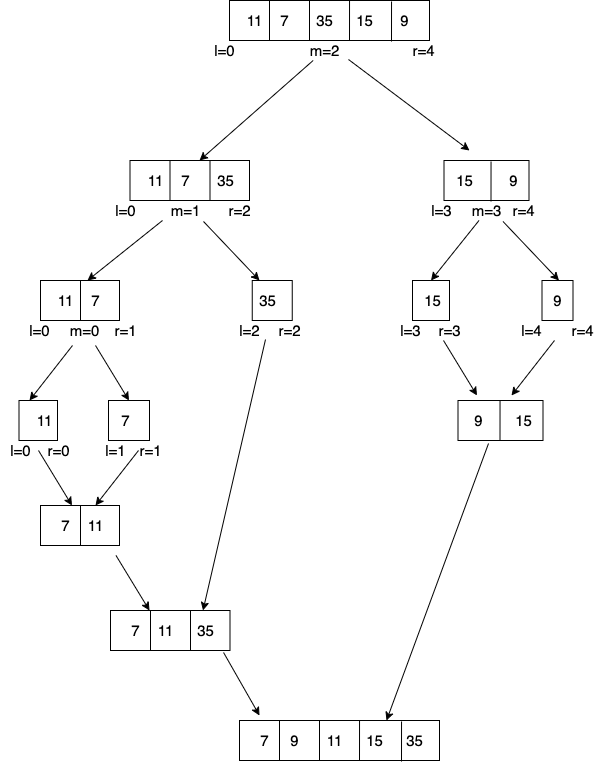
Merge Sort Analysis