Quick Sort

Partition a Given Array

Input: arr[] = {13, 16, 22, 20, 17}
pivot = 5
Output: arr[] = {13, 16, 17, 22, 20}
or
arr[] = {16, 13, 17, 22, 20} return value: 2
It is a new index of pivot element

Stability in Partition
├── Stable
│   └── Naive Partition
└── Not Stable
    ├── Lomuto Partition
    └── Hoare's Partition

Naive Partition

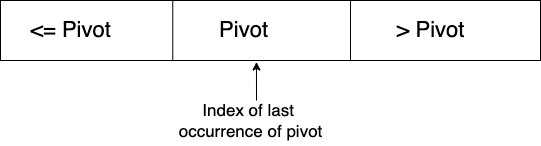
Input: arr[] = {12, 17, 18, 13, 17}
pivot = 1 or 4
Output: arr[] = {12, 13, 17, 17, 18} return value = 3

Note: Please note in the return value on above example that we return the last index of 17 i.e. 3, even our pivot is 1 or 4. So we need to return the last occurrence of pivot element as explained in above example.

Implementation

package main

import "fmt"

func main() {
    arr := []int{30, 80, 40, 90, 10, 50, 70}
    p := partition(arr, 0, len(arr)-1, len(arr)-1)
    fmt.Println(p) // 4
    fmt.Println(arr) // [30 40 10 50 70 80 90]
}

func partition(arr []int, l, h, p int) int {
    temp := make([]int, h-l+1) // create temp array
    idx := 0

    for i := l; i <= h; i++ {
        if arr[i] < arr[p] {
            temp[idx] = arr[i] //Smaller in temp array
            idx++
        }
    }

    for i := l; i <= h; i++ {
        if arr[i] == arr[p] {
            temp[idx] = arr[i] // equal elements in temp. We could do thi sin first loop but we need this loop for stability
            idx++
        }
    }

    res := l + idx - 1 // last ocurrance of pivot

    for i := l; i <= h; i++ {
        if arr[i] > arr[p] {
            temp[idx] = arr[i] // greator elements in temp
            idx++
        }
    }

    for i := l; i <= h; i++ {
        arr[i] = temp[i] // copy to original array
    }

    return res
}

Complexity

Time Complexity: θ(n)
Aux Space Complexity: θ(n)

Dry Run

arr[] = {5, 3, 12, 8, 5}
l=0, h=4, p=0

After 1st loop temp[] = {3, , , , }
After 2nd loop temp[] = {3, 5, 5, , }
After 3nd loop temp[] = {3, 5, 5, 12, 8}
After 4th loop arr[] = {3, 5, 5, 12, 8}

Lomuto Partition

arr[] = {10, 80, 30, 90, 40, 50, 70}
l=0, h=6, pivot=70

Lomuto partition always selects the last element s pivot element.

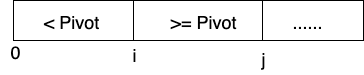
As above diagram explains, the Lomuto partition moves < pivot elements into 0 --> i section and keeps >=pivot elements intp i --> j section.

Implementation

package main

import "fmt"

func main() {
    arr := []int{30, 80, 10, 90, 40, 50, 70}
    p := lomutoPartition(arr, 0, len(arr)-1)
    fmt.Println(p)
    fmt.Println(arr)
}

func lomutoPartition(arr []int, l, h int) int {
    p := arr[h]
    i := l - 1
    for j := l; j < h; j++ {
        if arr[j] < p {
            i++
            arr[i], arr[j] = arr[j], arr[i]
        }
    }
    arr[i+1], arr[h] = arr[h], arr[i+1]
    return i + 1
}

Complexity

Time Complexity: O(n)
Aux Space Complexity: O(1)

Dry run

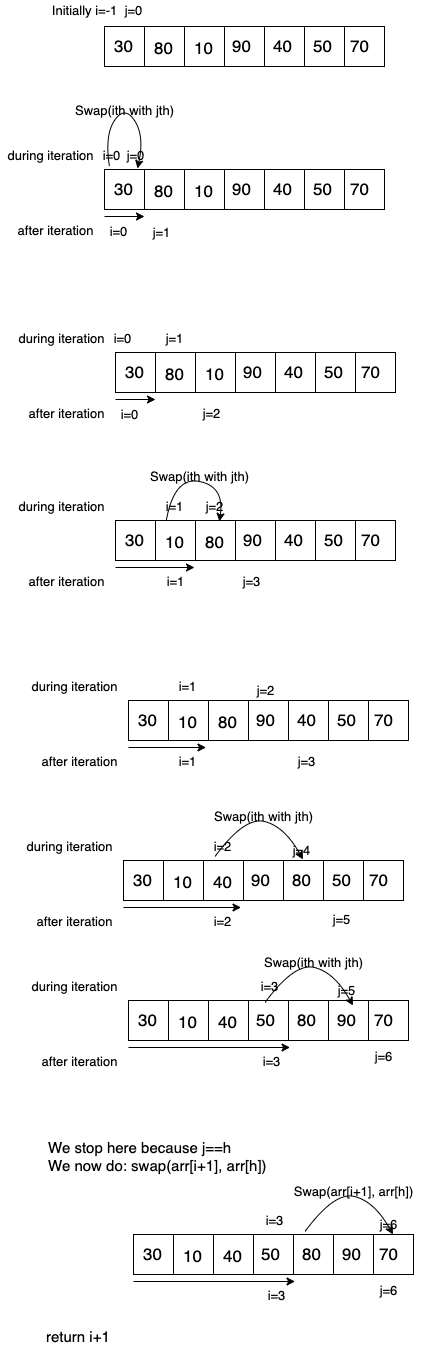
Cornor cases

Dry run yourself:

1. {70, 60, 80, 40, 30} ==> No small value than pivot
2. {30, 40, 20, 50, 80} ==> No large value than pivot